数组¶

参考：代码随想录数组内容

1. 数组介绍¶

数组是存放在连续内存空间上的相同类型数据的集合。

数组下标都是从0开始
数组内存空间的地址都是连续的

因为数组的内存空间地址都是连续的，所以在 删除或增添元素 的时候，就难免要移动其他元素的地址。

例如删除下标为3的元素，需要对下标为3的元素后面的所有元素都要做移动操作，如图所示：

即数组的元素不能删除，只能覆盖

2. 二分查找¶

使用二分查找的前提： - 数组为有序数组 - 数组中无重复元素（有重复元素的话，寻找到的满足题目要求的元素可能不唯一）

二分查找的边界问题：

遵循循环不变量的原则：在二分查找的过程中，保持不变量，即在while寻找中每一次边界的处理都要坚持根据区间的定义来操作，这就是循环不变量规则

二分查找中的区间定义有两种方式：

左闭右闭：[left, right] (说明右边的元素能够被选中，因此应该是 left <= right )
左闭右开：[left, right) (说明右边的元素无法被选中, 因此应该是 left < right)

2.1 二分查找¶

link : LeetCode 704

方法一：暴力

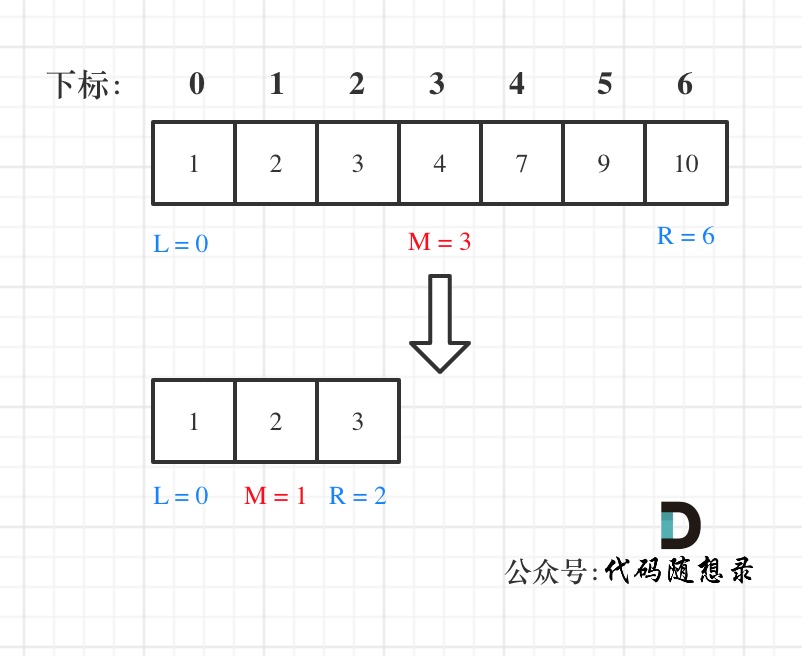
方法二：左闭右闭

图示：在数组：1,2,3,4,7,9,10中查找元素2，

class Solution {

    public int search(int[] nums, int target) {

        int left = 0, right = nums.length-1;

        // 采用左闭右闭的写法

        // 即 需要满足题目的条件在一个左闭右闭的区间中

        while(left <= right){

            int mid = (left + right) / 2;



            if (nums[mid] < target) left = mid + 1;

            else if (nums[mid] > target) right = mid - 1;

            else return mid;    
        }
        return -1;
    }

}

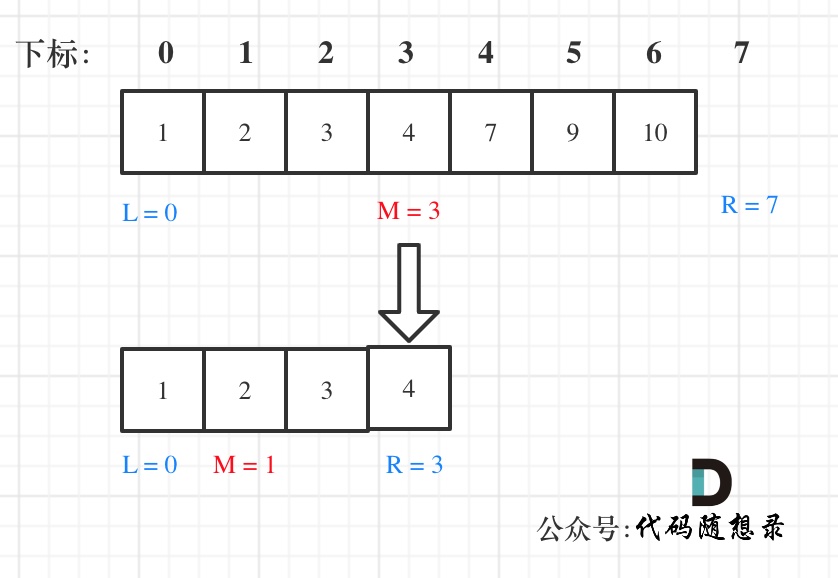
方法三：左闭右开

图示：

class Solution {

    public int search(int[] nums, int target) {

        int left = 0, right = nums.length-1;

        // 采用左闭右开的写法

        // 即 需要满足题目的条件在一个左闭右开的区间中

        // 因为左闭右开, right不能被选中

        while(left < right){

            int mid = (left + right) / 2;



            if (nums[mid] < target) left = mid + 1;

            // 因为 nums[mid] 肯定不满足条件, 但是right不能被选中, 所以 righ = mid

            else if (nums[mid] > target) right = mid;

            else return mid;    

        }



        return -1;

    }

}

3. 移除元素(快慢双指针)¶

link : LeetCode 27

思考:

数组中的元素的内存地址是连续的,不能直接删除某一个元素, 只能覆盖

暴力:

两层for循环，一个for循环遍历数组元素，当遇到目标元素后；第二个for循环更新数组（该元素后面的元素统一向前移动一位）。

双指针：

快慢指针法：通过一个快指针和慢指针在一个for循环下完成两个for循环的工作。（需要仔细考虑）

快指针：寻找新数组的元素，即最终的新数组就是不含有目标元素的数组，所以就是寻找不等于 val 的元素（存储的也是下标）
慢指针：指向新数组的下标（用来存储快指针指向的非val元素）

图示：

class Solution {

    public int removeElement(int[] nums, int val) {

        int fastIndex = 0, slowIndex = 0;

        // 快指针需要遍历 整个原数组, 从而找到所有不等于val的元素

        while(fastIndex < nums.length){

            if (nums[fastIndex] != val){

                nums[slowIndex] = nums[fastIndex];

                fastIndex++;

                slowIndex++;    

            }else{

                fastIndex++;

            }

        }

        return slowIndex;

    }

}

4. 有序数组的平方 (相向双指针)¶

link: LeetCode 977

暴力：

双指针（相向双指针）：

数组一开始是有序的，但是负数平方之后变成了最大数，所以数组平方后的最大值要么在原数组的最左边，要么在原数组的最右边，从而采用相向指针

class Solution {

    public int[] sortedSquares(int[] nums) {

        int n = nums.length;

        int res[] = new int[n];

        int size = n-1;

        // 使用双指针, 相向指针

        // left 指针从左边开始, right指针从右边开始

        int left = 0, right = n-1;

        while(left <= right){

            if (nums[left]*nums[left] > nums[right] * nums[right]) {

                res[size] = nums[left] * nums[left];

                left++;

                size--;

            }else{

                res[size] = nums[right] * nums[right];

                right--;

                size--;

            }

        }



        return res;



    }

}

关于循环中是 \(<=\) 还是 \(<\) : - 可以先模拟一遍，发现最后当 left=right的时候，正好是中间的值，需要进行处理； - 也可以直接运行，然后调试

5. 长度最小的子数组（滑动窗口）¶

link: LeetCode 59

暴力：

滑动窗口：

所谓滑动窗口，就是不断的调节子序列的起始位置和终止位置，从而得出我们要想的结果

在暴力解法中，是一个for循环滑动窗口的起始位置，一个for循环为滑动窗口的终止位置，用两个for循环完成了一个不断搜索区间的过程。

滑动窗口如何用一个for循环来完成这个操作？

首先要思考如果用一个for循环，那么应该表示滑动窗口的起始位置，还是终止位置。

如果只用一个for循环来表示滑动窗口的起始位置，那么如何遍历剩下的终止位置？此时难免再次陷入暴力解法的怪圈。

所以 只用一个for循环，那么这个循环的索引，一定是表示滑动窗口的终止位置。那么滑动窗口的起始位置如何移动呢？

图示：s=7，数组是 2，3，1，2，4，3，

实现滑动窗口的要素：

窗口内是什么？
如何移动窗口的起始位置？
如何移动窗口的结束位置？

窗口就是满足其和 ≥ s 的长度最小的连续子数组。

窗口的起始位置如何移动：如果当前窗口的值大于s了，窗口就要向前移动了（也就是该缩小了）。（只要窗口内满足题目条件, 就需要一直移动起始位置, 即一直缩小窗口, 直到窗口内不满足条件为止, 从而得到最小的窗口）

窗口的结束位置如何移动：窗口的结束位置就是遍历数组的指针，也就是for循环里的索引。

class Solution {

    public int minSubArrayLen(int target, int[] nums) {

       // 因为有一个子区间满足题目条件

       // 所以使用滑动窗口

       int left=0, right=0;

       // 定义窗口内的数值和

       int sum = 0;

       // 定义窗口的长度, 因为要求最小长度, 定义一个超大值

       int len = 100010;



       // 滑动窗口需要经过整个数组, 即窗口右边到数组最右端终止

       for (;right<nums.length; right++){

           // 首先窗口是第一个数组

           sum += nums[right];

           // 当窗口满足条件的时候, 持续缩小窗口, 直到不满足条件, 从而找到一个最小的子区间

           while(sum >= target){

               // 取最小值

               len = len< right-left+1?len: right-left+1;

               sum -= nums[left];

               left++;
           }
       }
       return len < 100010?len:0;

    }

}

6. 螺旋矩阵¶

link: LeetCode 59

思考：

在进行矩阵模拟的时候, 也需要坚持循环不变量的原则

模拟顺时针画矩阵的过程:

填充上行从左到右
填充右列从上到下
填充下行从右到左
填充左列从下到上

由外向内一圈一圈这么画下去。

这里一圈下来，我们要画每四条边，这四条边怎么画，每画一条边都要坚持一致的左闭右开，或者左开右闭的原则，这样这一圈才能按照统一的规则画下来。（即在循环中坚持循环不变量）

按照左闭右开的原则，图示：

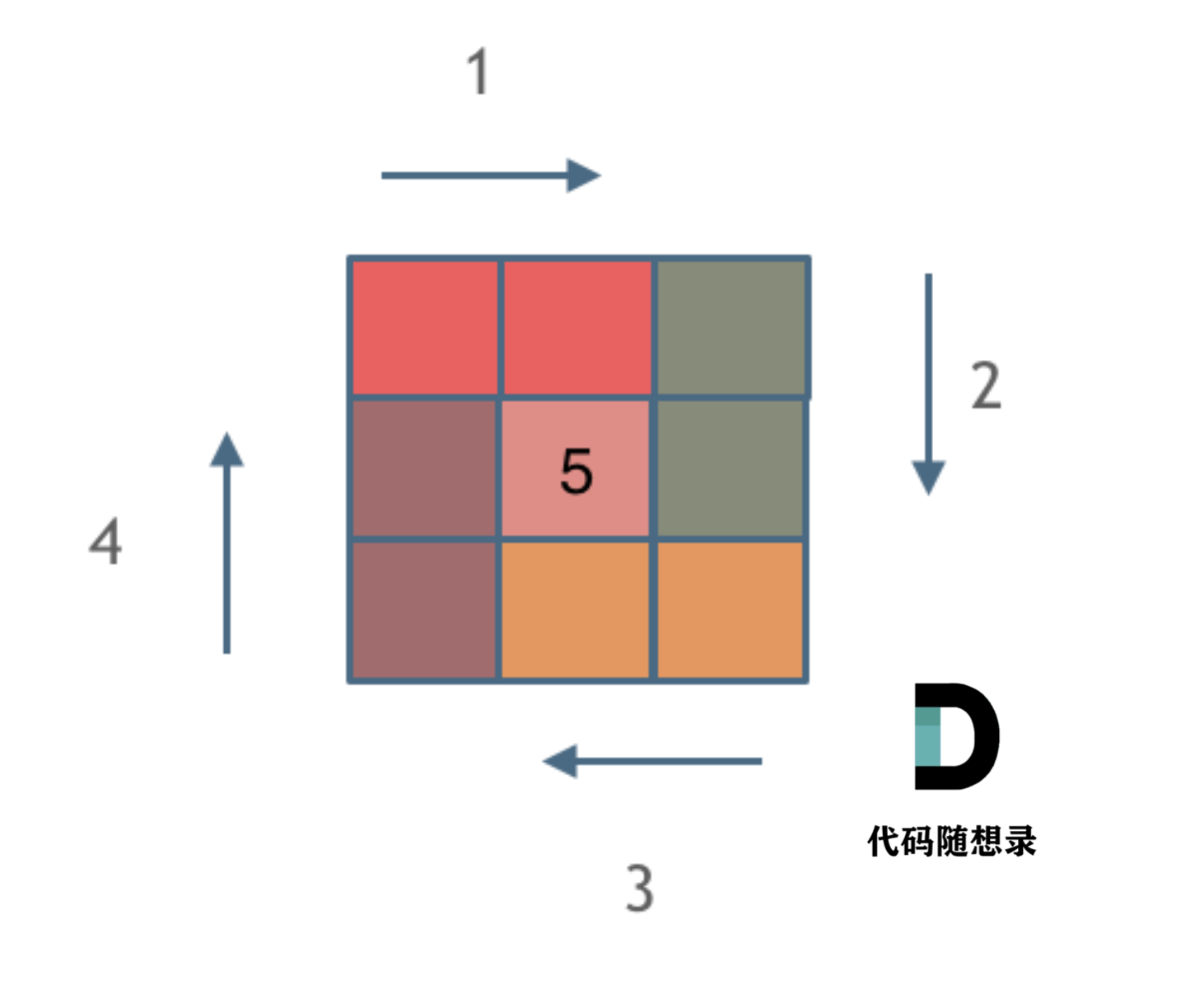
同时，进行模拟矩阵，需要首先确定的要素：

每一圈的起始位置的 x 和 y
能够循环多少圈
定义 offset 控制每一条边的遍历长度，每循环一次右边界收缩一位
矩阵中心位置(非必须)

class Solution {

    public int[][] generateMatrix(int n) {

        // 起始位置

        int startx = 0, starty = 0;

        // 圈数

        int loop= n /2;

        // 长度控制

        int offset = 1; // 左开右闭



        // 中心位置

        int mid = n/2;



        int res[][] = new int[n][n];



        int count = 1;



        while(loop-- > 0){

            int i=startx, j=starty;

            // 从左向右

            for (;j < n-offset; j++)

                res[i][j] = count++;

            // 从上到下

            for (;i < n-offset; i++)

                res[i][j] = count++;



            // 从右向左

            for (; j > starty; j--)

                res[i][j] = count++;



            for (; i > startx; i--)

                res[i][j] = count++;




            startx++;

            starty++;



            offset++;





        }



        // 如果有正中心

        if ( n % 2 != 0) res[startx][starty] = count;



        return res;

    }

}