ACWing 算法

数组¶

二分查找¶

题目链接：LeetCode、二分查找

给定一个 \(n\) 个元素有序的（升序）整型数组 \(nums\) 和一个目标值 \(target\) ，写一个函数搜索 \(nums\) 中的 \(target\)，如果目标值存在返回下标，否则返回 \(-1\)。

示例 1:

输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4

示例 2:

输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1

提示：

你可以假设 \(nums\) 中的所有元素是不重复的。
\(n\) 将在 \([1, 10000]\)之间。
\(nums\) 的每个元素都将在 \([-9999, 9999]\)之间。

解题思路¶

暴力：

class Solution {
    public int search(int[] nums, int target) {
        for (int i=0; i<nums.length; i++){
            if (nums[i] == target) return i;
        }
        return -1;
    }
}

二分：

class Solution {
    public int search(int[] nums, int target) {
        // 左闭右闭
        int left = 0, right = nums.length - 1;
        int mid = (left + right) / 2;
        while(left <= right){
            if (nums[mid] > target) right = mid-1;
            else if (nums[mid] < target) left = mid + 1;
            else return mid;

            mid = (left + right) / 2;
        }
        return -1;
    }
}

参考：¶

来自代码随想录

思路¶

这道题目的前提是数组为有序数组，同时题目还强调数组中无重复元素，因为一旦有重复元素，使用二分查找法返回的元素下标可能不是唯一的，这些都是使用二分法的前提条件，当大家看到题目描述满足如上条件的时候，可要想一想是不是可以用二分法了。

二分查找涉及的很多的边界条件，逻辑比较简单，但就是写不好。例如到底是 while(left < right) 还是 while(left <= right)，到底是right = middle呢，还是要right = middle - 1呢？

大家写二分法经常写乱，主要是因为对区间的定义没有想清楚，区间的定义就是不变量。要在二分查找的过程中，保持不变量，就是在while寻找中每一次边界的处理都要坚持根据区间的定义来操作，这就是循环不变量规则。

写二分法，区间的定义一般为两种，左闭右闭即[left, right]，或者左闭右开即[left, right)。

下面我用这两种区间的定义分别讲解两种不同的二分写法。

二分法第一种写法¶

第一种写法，我们定义 target 是在一个在左闭右闭的区间里，也就是[left, right] （这个很重要非常重要）。

区间的定义这就决定了二分法的代码应该如何写，因为定义target在[left, right]区间，所以有如下两点：

while (left <= right) 要使用 <= ，因为left == right是有意义的，所以使用 <=

if (nums[middle] > target) right 要赋值为 middle - 1，因为当前这个nums[middle]一定不是target，那么接下来要查找的左区间结束下标位置就是 middle - 1

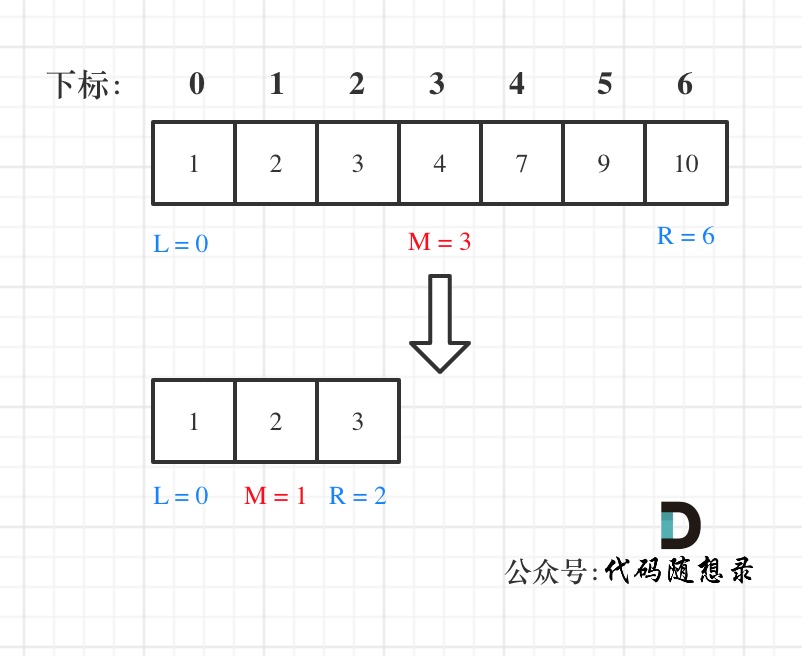
例如在数组：1,2,3,4,7,9,10中查找元素2，如图所示：

代码如下：（详细注释）
// 版本一
class Solution {
public:
    int search(vector<int>& nums, int target) {
        int left = 0;
        int right = nums.size() - 1; // 定义target在左闭右闭的区间里，[left, right]
        while (left <= right) { // 当left==right，区间[left, right]依然有效，所以用 <=
            int middle = left + ((right - left) / 2);// 防止溢出 等同于(left + right)/2
            if (nums[middle] > target) {
                right = middle - 1; // target 在左区间，所以[left, middle - 1]
            } else if (nums[middle] < target) {
                left = middle + 1; // target 在右区间，所以[middle + 1, right]
            } else { // nums[middle] == target
                return middle; // 数组中找到目标值，直接返回下标
            }
        }
        // 未找到目标值
        return -1;
    }
};
* 时间复杂度：O(log n) * 空间复杂度：O(1)

二分法第二种写法¶

如果说定义 target 是在一个在左闭右开的区间里，也就是[left, right) ，那么二分法的边界处理方式则截然不同。

有如下两点：

while (left < right)，这里使用 < ,因为left == right在区间[left, right)是没有意义的

if (nums[middle] > target) right 更新为 middle，因为当前nums[middle]不等于target，去左区间继续寻找，而寻找区间是左闭右开区间，所以right更新为middle，即：下一个查询区间不会去比较nums[middle]

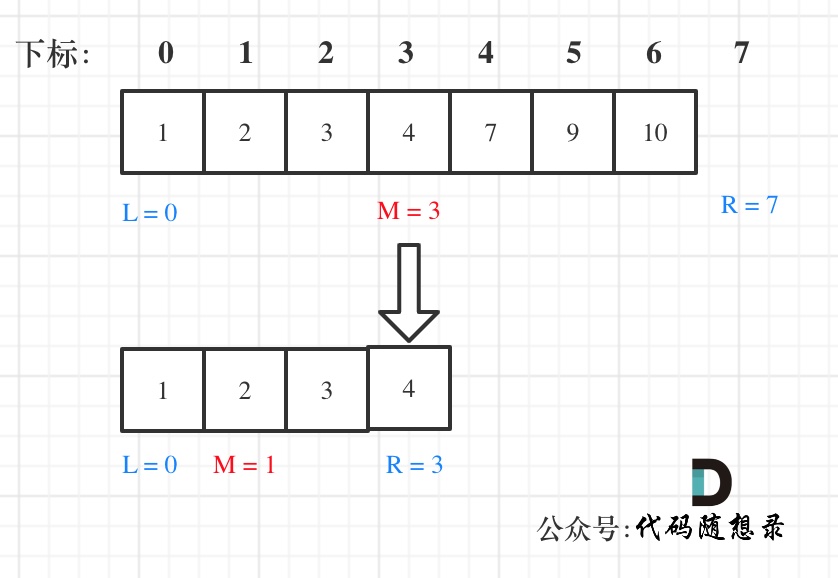
在数组：1,2,3,4,7,9,10中查找元素2，如图所示：（注意和方法一的区别）

代码如下：（详细注释）
// 版本二
class Solution {
public:
    int search(vector<int>& nums, int target) {
        int left = 0;
        int right = nums.size(); // 定义target在左闭右开的区间里，即：[left, right)
        while (left < right) { // 因为left == right的时候，在[left, right)是无效的空间，所以使用 <
            int middle = left + ((right - left) >> 1);
            if (nums[middle] > target) {
                right = middle; // target 在左区间，在[left, middle)中
            } else if (nums[middle] < target) {
                left = middle + 1; // target 在右区间，在[middle + 1, right)中
            } else { // nums[middle] == target
                return middle; // 数组中找到目标值，直接返回下标
            }
        }
        // 未找到目标值
        return -1;
    }
};
* 时间复杂度：O(log n) * 空间复杂度：O(1)

总结¶

二分法是非常重要的基础算法，为什么很多同学对于二分法都是一看就会，一写就废？

其实主要就是对区间的定义没有理解清楚，在循环中没有始终坚持根据查找区间的定义来做边界处理。

区间的定义就是不变量，那么在循环中坚持根据查找区间的定义来做边界处理，就是循环不变量规则。

本篇根据两种常见的区间定义，给出了两种二分法的写法，每一个边界为什么这么处理，都根据区间的定义做了详细介绍。

相信看完本篇应该对二分法有更深刻的理解了。

二分查找相关题目¶

搜索插入位置¶

题目来源：LeetCode , 代码随想录

解题思路

暴力

class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
        // 暴力
        for(int i=0; i<nums.size(); i++){
            if (nums[i] == target) return i;
            else if (nums[i] > target) return i;
        }
        return nums.size();
    }
};

二分

class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
        // 使用 左闭右闭 的思路
        int left = 0, right = nums.size()-1;
        int mid = (left + right) / 2;
        while(left <= right){
            if (nums[mid] > target) right = mid-1;
            else if(nums[mid] < target) left = mid+1;
            else return mid;
            mid = (left + right) / 2;
        }

        // 左闭右闭, 最终的mid会被采用到
        if (nums[mid] < target) return mid+1;
        // else if (nums[mid] > target && mid > 0) return mid-1;
        // else if  (nums[mid] > target && mid == 0) return 0;

        return 0;
    }
};

参考

思路¶

这道题目不难，但是为什么通过率相对来说并不高呢，我理解是大家对边界处理的判断有所失误导致的。

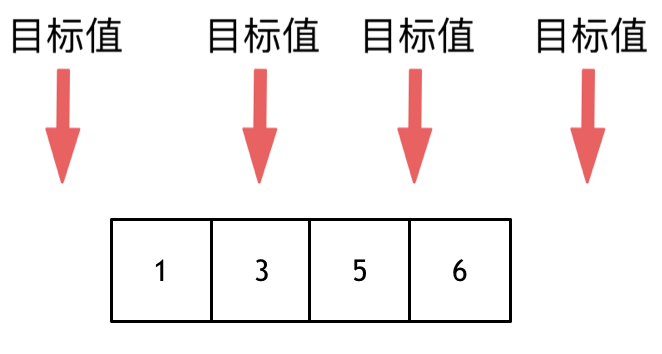
这道题目，要在数组中插入目标值，无非是这四种情况。

目标值在数组所有元素之前

目标值等于数组中某一个元素

目标值插入数组中的位置

目标值在数组所有元素之后

这四种情况确认清楚了，就可以尝试解题了。

接下来我将从暴力的解法和二分法来讲解此题，也借此好好讲一讲二分查找法。

暴力解法¶

暴力解题不一定时间消耗就非常高，关键看实现的方式，就像是二分查找时间消耗不一定就很低，是一样的。

C++代码
class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
        for (int i = 0; i < nums.size(); i++) {
        // 分别处理如下三种情况
        // 目标值在数组所有元素之前
        // 目标值等于数组中某一个元素
        // 目标值插入数组中的位置
            if (nums[i] >= target) { // 一旦发现大于或者等于target的num[i]，那么i就是我们要的结果
                return i;
            }
        }
        // 目标值在数组所有元素之后的情况
        return nums.size(); // 如果target是最大的，或者 nums为空，则返回nums的长度
    }
};
时间复杂度：O(n)

空间复杂度：O(1)

效率如下：

二分法¶

既然暴力解法的时间复杂度是O(n)，就要尝试一下使用二分查找法。

大家注意这道题目的前提是数组是有序数组，这也是使用二分查找的基础条件。

以后大家只要看到面试题里给出的数组是有序数组，都可以想一想是否可以使用二分法。

同时题目还强调数组中无重复元素，因为一旦有重复元素，使用二分查找法返回的元素下标可能不是唯一的。

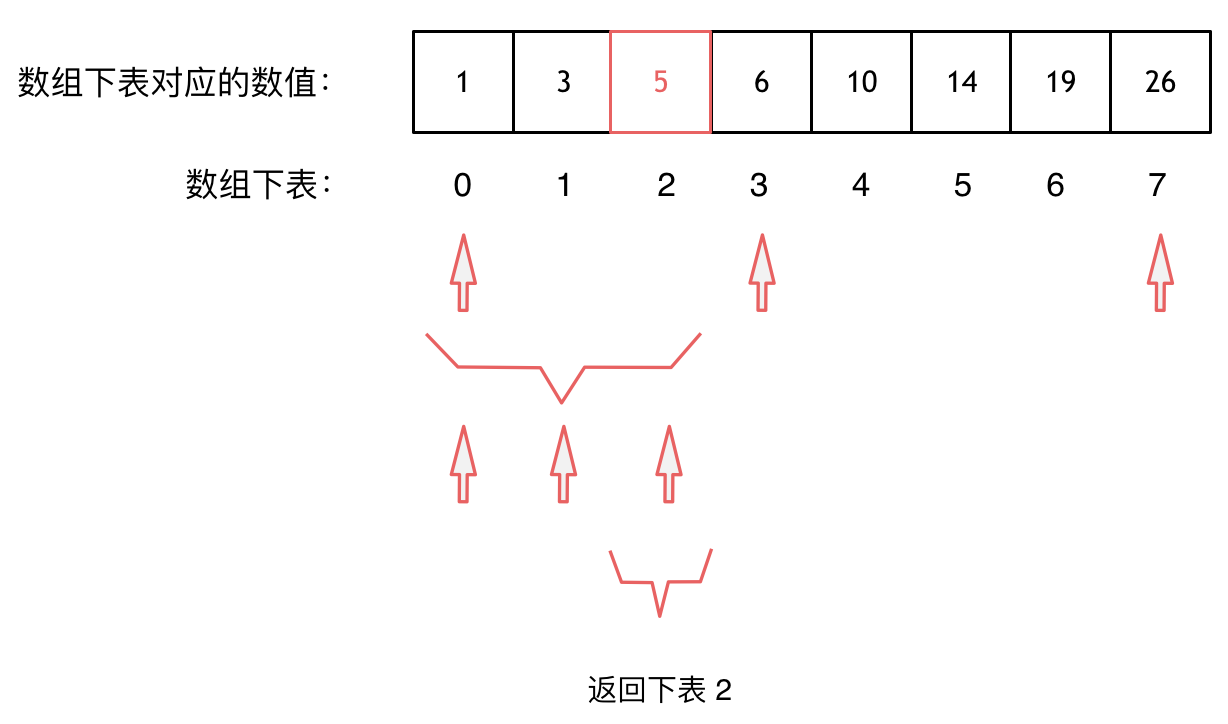
大体讲解一下二分法的思路，这里来举一个例子，例如在这个数组中，使用二分法寻找元素为5的位置，并返回其下标。

二分查找涉及的很多的边界条件，逻辑比较简单，就是写不好。

相信很多同学对二分查找法中边界条件处理不好。

例如到底是 while(left < right) 还是 while(left <= right)，到底是right = middle呢，还是要right = middle - 1呢？

这里弄不清楚主要是因为对区间的定义没有想清楚，这就是不变量。

要在二分查找的过程中，保持不变量，这也就是循环不变量 （感兴趣的同学可以查一查）。

二分法第一种写法¶

以这道题目来举例，以下的代码中定义 target 是在一个在左闭右闭的区间里，也就是[left, right] （这个很重要）。

这就决定了这个二分法的代码如何去写，大家看如下代码：

大家要仔细看注释，思考为什么要写while(left <= right)，为什么要写right = middle - 1。
class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
        int n = nums.size();
        int left = 0;
        int right = n - 1; // 定义target在左闭右闭的区间里，[left, right]
        while (left <= right) { // 当left==right，区间[left, right]依然有效
            int middle = left + ((right - left) / 2);// 防止溢出 等同于(left + right)/2
            if (nums[middle] > target) {
                right = middle - 1; // target 在左区间，所以[left, middle - 1]
            } else if (nums[middle] < target) {
                left = middle + 1; // target 在右区间，所以[middle + 1, right]
            } else { // nums[middle] == target
                return middle;
            }
        }
        // 分别处理如下四种情况
        // 目标值在数组所有元素之前  [0, -1]
        // 目标值等于数组中某一个元素  return middle;
        // 目标值插入数组中的位置 [left, right]，return  right + 1
        // 目标值在数组所有元素之后的情况 [left, right]， 因为是右闭区间，所以 return right + 1
        return right + 1;
    }
};
时间复杂度：O(log n)

空间复杂度：O(1)

效率如下：

二分法第二种写法¶

如果说定义 target 是在一个在左闭右开的区间里，也就是[left, right) 。

那么二分法的边界处理方式则截然不同。

不变量是[left, right)的区间，如下代码可以看出是如何在循环中坚持不变量的。

大家要仔细看注释，思考为什么要写while (left < right)，为什么要写right = middle。
class Solution {
public:
    int searchInsert(vector<int>& nums, int target) {
        int n = nums.size();
        int left = 0;
        int right = n; // 定义target在左闭右开的区间里，[left, right)  target
        while (left < right) { // 因为left == right的时候，在[left, right)是无效的空间
            int middle = left + ((right - left) >> 1);
            if (nums[middle] > target) {
                right = middle; // target 在左区间，在[left, middle)中
            } else if (nums[middle] < target) {
                left = middle + 1; // target 在右区间，在 [middle+1, right)中
            } else { // nums[middle] == target
                return middle; // 数组中找到目标值的情况，直接返回下标
            }
        }
        // 分别处理如下四种情况
        // 目标值在数组所有元素之前 [0,0)
        // 目标值等于数组中某一个元素 return middle
        // 目标值插入数组中的位置 [left, right) ，return right 即可
        // 目标值在数组所有元素之后的情况 [left, right)，因为是右开区间，所以 return right
        return right;
    }
};
时间复杂度：O(log n)

空间复杂度：O(1)

总结¶

希望通过这道题目，大家会发现平时写二分法，为什么总写不好，就是因为对区间定义不清楚。

确定要查找的区间到底是左闭右开[left, right)，还是左闭又闭[left, right]，这就是不变量。

然后在二分查找的循环中，坚持循环不变量的原则，很多细节问题，自然会知道如何处理了。

在排序数组中查找元素的第一个和最后一个位置¶

题目来源：LeetCode, 代码随想录

解题思路

暴力

class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int target) {
        // 定义目标元素在数组中的左右边界
        int left=-1, right=-1;
        for (int i=0; i<nums.size(); i++){
            // 如果左右边界都未赋值，先给左边界赋值
            if (left==-1 && right==-1 && nums[i] == target) left = i;
            // 如果左边界已经赋值, 给右边界赋值
            if (left!=-1 && nums[i] == target) right = i; 
        }
        // 如果右边界最后都未赋值, 使其等于左边界
        if (right==-1) right = left;

        return {left, right};

    }
};

移动元素（双指针）¶

题目来源：LeetCode27, 代码随想录

解题思路¶

暴力

class Solution {
public:
    int removeElement(vector<int>& nums, int val) {
        // 直接暴力
        // 双层循环, 第一层遍历数组, 寻找和val相同的元素
        // 第二层循环更新数组, 当找到和val相同的元素后, 将其后面的元素向前移动一位
        int size = nums.size();
        for (int i=0; i<size; i++){
            if (nums[i] == val){
                for (int j=i; j<size-1;j++){
                    nums[j]=nums[j+1];
                }
                size--;
                i--;
            }
        }

        return size;
    }
};

双指针(快慢双指针)

class Solution {
public:
    int removeElement(vector<int>& nums, int val) {
        // 双指针
        // 快指针：寻找新数组的元素(不包含val)
        // 慢指针：指向更新 新数组 的下标位置
        int slowIndex=0, fastIndex=0;

        int size = nums.size();
        while(fastIndex < nums.size()){
            // 寻找新数组的元素
            // 当元素不等于val的时候, 说明新数组的前面几个元素与原数组相同
            if (nums[fastIndex] != val){
                nums[slowIndex] = nums[fastIndex];
                slowIndex++;
                fastIndex++;
            }else{
                fastIndex++;
            }
        }

        return slowIndex;
    }
};

双指针（相向指针）

class Solution {
public:
    int removeElement(vector<int>& nums, int val) {
        // 双指针(相向双指针)
        // 左边的指针 寻找数组中等于val的元素
        // 右边的指针寻找数组中不等于val的元素
        // 将两个元素交换位置, 从而使得左边的都是不等于val的元素

        int leftIndex=0, rightIndex=nums.size()-1;
        while(leftIndex <= rightIndex){
            // 左边的指针寻找等于val的元素
            // 必须确定 leftIndex <= rightIndex, 不然会产生索引非法的问题
            while(leftIndex <= rightIndex && nums[leftIndex]!=val) leftIndex++;
            // 右边的指针寻找不等于val的元素
            while(leftIndex <= rightIndex && nums[rightIndex]==val) rightIndex--;

            if (leftIndex < rightIndex){
                // 进行交换
                int temp = nums[leftIndex];
                nums[leftIndex] = nums[rightIndex];
                nums[rightIndex] = temp;

                leftIndex++; rightIndex--;
            }

        }
        return leftIndex;

    }
};

双指针相关题目¶

删除有序数组中的重复项¶

题目来源：LeetCode

思路

两个关键点：

非严格递增排列，数组是有序且递增的，说明重复的元素是相邻的
原地删除重复出现的元素，说明可以原地修改数组
题目要求：元素的相对顺序保持一致（说明不能改变数组的稳定性，不能使用相向指针）

代码

class Solution {
public:
    int removeDuplicates(vector<int>& nums) {
        // 因为要保持相对顺序一致, 因此不能使用相向指针
        // 使用快慢指针
        // 快指针寻找不重复的元素, 慢指针是新数组的索引
        int slowIndex = 0, fastIndex=1;
        while(fastIndex < nums.size()){
           // 当相邻的元素不相同的时候, 直接复制快指针指向的元素
           while(fastIndex < nums.size() && nums[slowIndex] != nums[fastIndex]){
               nums[slowIndex+1]=nums[fastIndex];
               slowIndex++;
               fastIndex++;
           }
           // 当相邻的元素重复时，只移动快指针, 寻找下一个不重复的元素
            while(fastIndex < nums.size() && nums[slowIndex] == nums[fastIndex]){
                fastIndex++;
            }
        }

        return slowIndex+1;

    }
};

有序数组的平方¶

题目来源：LeetCode977, 代码随想录

解题思路¶

暴力

class Solution {
public:
    vector<int> sortedSquares(vector<int>& nums) {
        // 先平方
        for (int i=0;i<nums.size();i++){
            nums[i] = nums[i]*nums[i];
        }
        // 后排序  
        sort(nums.begin(),nums.end());
        return nums;
    }
};

双指针

原数组是按照非递减顺序排列（即原数组是有序的）
将原数组进行平方, 最大的值要么在最左边，要么在最右边

class Solution {
public:
    vector<int> sortedSquares(vector<int>& nums) {
        // 使用双指针
        int left=0, right=nums.size()-1;
        // 定义一个和nums相同大小的数组
        vector<int> res(nums.size(), 0);
        // k指向新数组的最后位置
        int k = nums.size()-1;

        while(left <= right){
            if (nums[left] * nums[left] > nums[right]*nums[right]){
                res[k--] = nums[left] * nums[left];
                left++;
            }                
            else{
                res[k--] = nums[right] * nums[right];
                right--;
            }

        }

        return res;
    }
};

长度最小的子数组¶

题目来源：LeetCode209, 代码随想录

解题思路¶

暴力

class Solution {
public:
    int minSubArrayLen(int target, vector<int>& nums) {
            // 暴力
            // sum 保存子序列的和, res保存子序列的长度(一开始设置res为超大值, 从而当子序列的长度小于之前保存的子序列的长度的时候, 更新res)
            int sum=0, res=1000000;
            for(int i=0;i<nums.size();i++){
                // 开始寻找新的子序列, sum更新为0
                sum=0;
                for(int j=i;j<nums.size();j++){
                    sum += nums[j];
                    // 当子序列的和满足条件(判断新的子序列和之前存储的子序列的长度)
                    if (sum >= target){
                        // 如果新的子序列的长度小于之前存储的子序列的长度, 则更新
                        if (res > j-i+1) res = j-i+1;
                        break;
                    }
                }
                // 如果第一次遍历整个数组, 发现整个数组的和都不满足条件, 则找不到满足条件的子序列
                if (res==1000000 && i==0) {
                    res=0;
                    break;
                }

            }

            return res;
    }
};

滑动窗口

class Solution {
public:
    int minSubArrayLen(int target, vector<int>& nums) {
        // 滑动窗口(双指针实现滑动窗口)
        // left表示窗口最左边, right表示窗口最右边
        int left=0, right=0;

        if (nums.size()==0) return 0;

        // sum: 窗口内的元素和, res: 窗口长度
        int sum=nums[0], res=100010;

        // 当窗口 最右边 还没有到数组最右边的时候
        while(right < nums.size()){
            // 如果窗口内的元素和 满足条件
            if(sum >= target){
                // 取 当前窗口 和之前窗口的最小值
                res = min(right-left+1, res);
                // 窗口左边向右移动, 右边不变, 窗口变小
                sum -= nums[left];
                left++;
                continue;

            }

            if (right == nums.size()-1) break;

            // 如果窗口内的元素和不满足条件, 窗口右边向右移动, 左边不变, 窗口变大
            right++;
            sum += nums[right];


        }
        // 如果整个数组都不满足条件, break
        if (res == 100010  && left==0 && right==nums.size()-1){
            res = 0;
        }

        return res;

    }
};

模拟栈¶

题目链接：https://www.acwing.com/problem/content/830/

实现一个栈，栈初始为空，支持四种操作：

push x – 向栈顶插入一个数 \(x\)；
pop – 从栈顶弹出一个数；
empty – 判断栈是否为空；
query – 查询栈顶元素。

现在要对栈进行 \(M\) 个操作，其中的每个操作 \(3\) 和操作 \(4\) 都要输出相应的结果。

输入格式¶

第一行包含整数 \(M\)，表示操作次数。

接下来 \(M\) 行，每行包含一个操作命令，操作命令为 push x，pop，empty，query 中的一种。

输出格式¶

对于每个 empty 和 query 操作都要输出一个查询结果，每个结果占一行。

其中，empty 操作的查询结果为 YES 或 NO，query 操作的查询结果为一个整数，表示栈顶元素的值。

数据范围¶

\(1 \le M \le 100000\), \(1 \le x \le 10^9\) 所有操作保证合法。

输入样例：¶

10
push 5
query
push 6
pop
query
pop
empty
push 4
query
empty

输出样例：¶

5
5
YES
4
NO

解题思路¶

#include <iostream>

using namespace std;

// 使用数组模拟栈, N 表示数组的大小
// 因为共有M次操作, 而 数据范围中 1≤M≤100000, 因此定义数组的大小为 100010
const int N = 100010;

// m 表示操作次数
int m;

// stk: 表示用来模拟栈的数组, tt: 栈顶索引
int stk[N], tt;


int main(){

    scanf("%d", &m);
    while(m){
        // op : 操作命令
        string op;
        // x : 如果是 push, x表示入栈的元素 
        int x;

        cin >> op;
        if (op == "push") {
            scanf("%d", &x);
            // 进行入栈操作
            stk[++tt] = x;

        }
        else if (op == "query"){
            cout << stk[tt] << endl;
        }
        else if (op == "pop"){
            // 弹出操作, 相当于将栈顶 索引减一
            // 先判断栈是否为空, 如果不为空, 则减一
            if (tt) tt--;
        }
        else if (op == "empty"){
            // 如果 tt=0, 表示为空
            if (!tt) cout << "YES" <<endl;
            else cout << "NO" <<endl;
        }

        m--;
    }


}

模拟队列¶

题目链接：https://www.acwing.com/problem/content/831/

实现一个队列，队列初始为空，支持四种操作：

push x – 向队尾插入一个数 \(x\)；
pop – 从队头弹出一个数；
empty – 判断队列是否为空；
query – 查询队头元素。

现在要对队列进行 \(M\) 个操作，其中的每个操作 \(3\) 和操作 \(4\) 都要输出相应的结果。

输入格式¶

第一行包含整数 \(M\)，表示操作次数。

接下来 \(M\) 行，每行包含一个操作命令，操作命令为 push x，pop，empty，query 中的一种。

输出格式¶

对于每个 empty 和 query 操作都要输出一个查询结果，每个结果占一行。

其中，empty 操作的查询结果为 YES 或 NO，query 操作的查询结果为一个整数，表示队头元素的值。

数据范围¶

\(1 \le M \le 100000\), \(1 \le x \le 10^9\), 所有操作保证合法。

输入样例：¶

10
push 6
empty
query
pop
empty
push 3
push 4
pop
query
push 6

输出样例：¶

NO
6
YES
4

解题思路：¶

#include <iostream>

using namespace std;

// N: 数组的大小
const int N = 100010;
// que: 使用数组 que 模拟队列
// hh: 队列头, tt: 队列尾部
int que[N], hh, tt=-1;

// m: 操作次数
int m;

int main(){
    cin >> m;
    while(m){
        // op 表示操作符
        string op;
        int x;


        cin >> op;
        if (op == "push"){
            cin >> x;
            que[++tt] = x;
        }
        else if (op == "query"){
            cout << que[hh] << endl;
        }
        else if (op == "pop"){
            // 弹出操作, 相当于把对头向后移动
            hh++;
        }
        else if (op == "empty"){
            if (hh <= tt) cout << "NO" << endl;
            else cout << "YES" <<endl;
        }


        m--;
    }



}

ACWing 算法

数组¶

二分查找¶

解题思路¶

参考：¶

思路¶

二分法第一种写法¶

二分法第二种写法¶

总结¶

二分查找相关题目¶

搜索插入位置¶

思路¶

暴力解法¶

二分法¶

二分法第一种写法¶

二分法第二种写法¶

总结¶

在排序数组中查找元素的第一个和最后一个位置¶

移动元素（双指针）¶

解题思路¶

双指针相关题目¶

删除有序数组中的重复项¶

有序数组的平方¶

解题思路¶

长度最小的子数组¶

解题思路¶

模拟栈¶

输入格式¶

输出格式¶

数据范围¶

输入样例：¶

输出样例：¶

解题思路¶

模拟队列¶

输入格式¶

输出格式¶

数据范围¶

输入样例：¶

输出样例：¶

解题思路：¶

评论